Mat
See Also: Mat for Beginners
The Mat (M) statement performs several array (or Matrix) operations. It can change the number of dimensions or elements, assign new values, and apply an expression to all elements. Each element is an individual variable.
MAT subarray operator
Arrays may now be subscripted with a starting and ending element number to process a portion of an array. This works much the same as Business Rules sub-string feature, except it works with elements instead of characters.
00100 MAT A(6:10)=B ! copies B(1)..B(5) into A(6)..A(10); 00110 MAT B=A(6:10) ! B dimensioned for 5 elements. 00120 MAT B(1:5)=A(6:10) ! Copy part of 1 array to part of another 00130 READ MAT A(1:5) ! only read elements 1-5 00140 PRINT FIELDS SF$:MAT A$(F:F+9) ! 10 elements starting at "F" are displayed
Multi-dimensional matrixes are not supported for sub-array processing.
Comments and Examples
Arrays and matrices are manipulated using the MAT statement. An array is a one-dimensional matrix. The MAT statement can be used to assign values to all elements of a matrix in a single statement. For example, MAT can be used to initialize all elements of an array to a constant as follows:
00100 MAT A = (0)
00200 MAT A$ = ("")
In the next example, values in one array are copied to another array:
00300 MAT A$ = B$ 00400 MAT A = B
The MAT statement also handles mathematical operations on numeric arrays. Two arrays may be added or subtracted as follows:
00100 MAT A = B + C 00200 MAT A = B - C
Line 100 adds each element of matrix B to the corresponding element of matrix C and stores the result in the corresponding element of matrix A. The dimensions of A, B and C must be the same.
Another form of matrix arithmetic involves combining a matrix and a scalar. Business Rules adding, subtracting, multiplying, and dividing a number by all elements of a matrix. It is important to note that the scalar (X in the following examples) must be the left operand, and the matrix (B) must be the right operand. Due to these restrictions, subtraction and division must be accomplished in the manner illustrated in lines 500 and 600 below:
00300 MAT A=(X)+B 00400 MAT A=(X)*B 00500 MAT A=(-X)+B 00600 MAT A=(1/X)*B
In line 300, the numeric expression inside the parentheses is added to every element of matrix B; the result is stored in matrix A.
Array sorting is another feature of the MAT statement. Both string and numeric arrays can be sorted in ascending (AIDX) or descending (DIDX) order. The following is an example of using MAT AIDX to sort an array of names. The names are stored in array N$ and the number of names used is stored in L. See the AIDX function for another example.
00100 DIM A(100), N$(100)*30 00200 MAT N$(L) 00300 MAT A(L)=AIDX(N$) 00400 FOR I=1 TO L 00500 PRINT N$(A(I)) 00600 NEXT I
Array A contains the indexed order of array N$, similar to the way an address-out sort file contains pointers to the original data. Lines 400 to 600 print the names in ascending order.
Lines 200 and 300 above illustrate another MAT function: redimensioning. The number of elements in an array or matrix can be increased or decreased. For example:
00100 DIM A(100), B(100) 00200 NA=200 00300 MAT A(NA) 00400 NB=50 00500 MAT B(NB) 00600 MAT A(NB)=B
Line 300 increases the number of elements of A to 200, and line 500 decreases the number of elements of B to 50. Line 600 illustrates copying array B into array A, while at the same time re-dimensioning A to have NB elements.
Re-dimensioning also allows you to change the number of dimensions. The following example changes matrix A from a 10 x 10 matrix to a one-dimensional array of 100 elements without changing the values of the elements of the matrix.
00100 DIM A(10,10) 00200 MAT A(100)=A
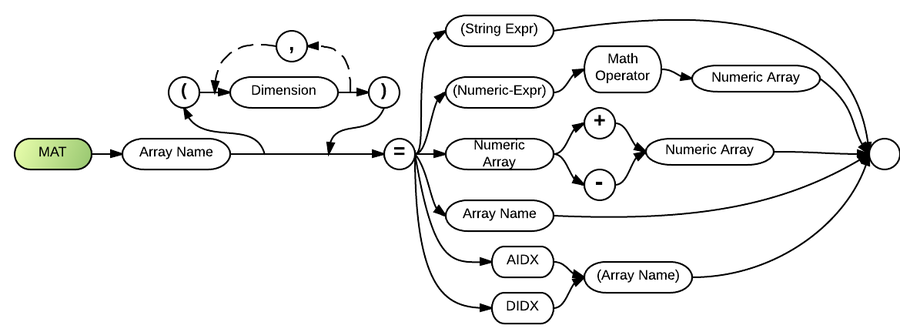
Syntax
MAT <array name> [(<dimension>[,...])] = {(<string expression>)| (<numeric expression>) <math operator> <numeric array> | <numeric array> +|- <numeric array> | <array name> | AIDX(<array name>)| DIDX(<array name>)}
Defaults
- No re-dimension.
- No assignment.
- Set the value of all elements to the expression.
Parameters
"Array-name" is a required parameter that represents a numeric or string array name. The optional "dimension" parameter is used to change the dimensions of the array mentioned in "array-name". Each dimension specification identifies the maximum size for that dimension. The dimension parameter is exactly the same as a combination of the "rows" and "columns" parameters described with the DIM statement, with the important distinction that any type of numeric expression may be used -not just integer constants.
"String-expr" can be used to set all the elements of an array to the same character string.
"Numeric-expr" represents expressions to be evaluated to a single value, which are used to make assignments to the matrix elements. It may be followed by one of four allowable "math operator" parameters: +, -, * or /. The math operator must then be followed by a "numeric array".
"Numeric array" is used in varieties of the MAT statement that perform arithmetic on arrays.
"AIDX" and "DIDX" are keywords used to invoke array functions for sorting an array in ascending (AIDX) or descending (DIDX) order. Both must be followed by an "array-name" within parentheses. Both create an index array, which is a numeric array containing numbers to be used as subscripts for accessing the original array in a sorted order. AIDX and DIDX can be used to sort either numeric or string arrays.
Technical Considerations
- Using re-dimensioning to decrease the number of elements saves memory and speeds up the AIDX and DIDX functions.
- When one matrix is assigned to another (via arithmetic or the AIDX/DIDX functions) the assigned-to matrix must be the same size as the assigned-from matrix. In the case of string matrices, the assigned-to matrix must have the same string length dimension as the assigned-from matrix; a SOFLOW condition will occur if the assigned-to string is too short.
- The expression to the right of the equal sign must be the same type (either numeric or string) as the array named on the left side.
- Re-dimensioning can increase or decrease the number of elements or the number of dimensions, but it cannot change the maximum lengths of string arrays.
- Use PRINT with the MAT keyword to print a matrix.
- Use READ with the MAT keyword to read data into an entire array.
- When matrixes are re-dimensioned, data is always preserved. When the size of a matrix is increased, the added elements are set to zero or null.
- Use CHAIN with the MAT keyword to chain an array assignment. (See the CHAIN statement for more information.)
- See the AIDX and DIDX Functions for more information.
Practical Uses
Mat can be used with read and data statements to put a lot of information into and easy to use array. For example, keeping forms together:
00100 data "8,2,c 6","8,9,c 30","8,39,c 1","8,40,c 30","9,2,c 9","9,12,c 30","9,43,c 6","9,50,c 15","9,65,c 7","9,73,c 2","10,2,c 9","10,12,c 7" 00110 read Mat Prinform$ ... 00210 print fields Mat Prinform$: "Name: ",First$," ",Last$,"Address: ",Address$,"City: ",City$,"State: ",State$,"Zipcode: ",Zipcode$
Another common use is reading data from a file into arrays to print into a GRID:
00020 print Newpage 00030 dim Headings$(10), Widths(10), Forms$(10), Answers$(6)*30,Ordered(3), Head 00040 data "First Name","Last Name","Address","City","State","Zip Code","Shipping","Item 1","Item 2","Item 3" 00050 read Mat Headings$ 00060 data 10,10,10,10,4,9,3,3,3,3 00070 read Mat Widths 00080 data "cc 30","cc 30","cc 30","cc 15","cc 2","cc 7","cc 1","n 1","n 1","n 1" 00090 read Mat Forms$ 00100 ! 00110 dim Firstname$(1)*30,Lastname$(1)*30,Address$(1)*30,City$(1)*15,State$(1)*2,Zipcodes$(1)*7,Shipmethod$(1)*1 00120 ! 00130 open #1: "name=orders.INT,kfname=lastfirst.int, recl=118,kps=31/1,kln=30/30,USE", internal, outin, keyed 00140 ! 00150 mat Firstname$(0) 00160 mat Lastname$(0) 00170 mat Address$(0) 00180 mat City$(0) 00190 mat State$(0) 00200 mat Zipcodes$(0) 00210 mat Shipmethod$(0) 00270 ! 00280 READTHENEXTONE: ! Ok 00290 read #1, using RECFORM: Mat Answers$,Shipping$,Mat Ordered eof DONEREADING 00300 RECFORM: form C 30,C 30,C 30,C 15,C 2,C 7,C 1,N 1,N 1,N 1 00310 ! 00320 let Newsize=Udim(Firstname$)+1 00330 ! 00340 mat Firstname$(Newsize) 00350 mat Lastname$(Newsize) 00360 mat Address$(Newsize) 00370 mat City$(Newsize) 00380 mat State$(Newsize) 00390 mat Zipcodes$(Newsize) 00400 mat Shipmethod$(Newsize) 00450 ! 00460 let Firstname$(Newsize)=uprc$(Answers$(1)) 00470 let Lastname$(Newsize)=Answers$(2) 00480 let Address$(Newsize)=Answers$(3) 00490 let City$(Newsize)=Answers$(4) 00500 let State$(Newsize)=Answers$(5) 00510 let Zipcodes$(Newsize)=Answers$(6) 00520 let Shipmethod$(Newsize)=Shipping$ 00570 ! 00580 goto READTHENEXTONE 00590 ! 00600 DONEREADING: ! We're done reading, go to the nexst part, print them on the list 00610 ! 00620 print fields "2,2,grid 10/80,headers": (Mat Headings$,Mat Widths,Mat Forms$) 00630 print fields "2,2,grid 10/80,=r": (Mat Firstname$, Mat Lastname$,Mat Address$,Mat City$,Mat State$,Mat Zipcodes$,Mat Shipmethod$,Mat Item1,Mat Item2,Mat Item3)
Sorting Multidimensional Arrays
The following program illustrates using AIDX to sort both one dimensional arrays and two dimensional arrays. In the multi-dimensional example five rows of three strings are sorted by the first column of each row. The trick here is to select a key column and keep each row intact when transferring to another (sorted) array.
00010 ! Replace Aidx_Demo
00020 !
00030 ! Sample Code For Using Aidx
00040 !
00050 ! Last Revised 05/24/17
00060 !
00070 dim ONE_DIM1$(10)*100,TWO_DIM1$(5,3)*100,INDEX(1)
00080 dim ONE_DIM2$(10)*100,TWO_DIM2$(5,3)*100,WORK$(1)*100
00090 !
00100 execute "con console data_only" !Keep console on during kstat
00110 let RND(555) !Same random numbers each run
00120 !
00130 ! ***** One Dimenional Sort
00140 for X = 1 to UDIM(ONE_DIM1$)
00150 let ONE_DIM1$(X) = STR$(RND)
00160 next X
00170 print MAT ONE_DIM1$
00180 print
00190 !
00200 mat INDEX(UDIM(ONE_DIM1$)) = AIDX(ONE_DIM1$)
00210 for X = 1 to UDIM(ONE_DIM1$)
00220 let ONE_DIM2$(X) = ONE_DIM1$(INDEX(X))
00230 next X
00240 print MAT ONE_DIM2$
00250 print
00260 print "Press Any Key..."
00270 let KSTAT$(1)
00280 !
00290 ! ***** Two Dimensional Sort
00300 for X = 1 to UDIM(TWO_DIM1$,1)
00310 for Y = 1 to UDIM(TWO_DIM1$,2)
00320 let TWO_DIM1$(X,Y) = STR$(RND) !Load random data
00330 next Y
00340 next X
00350 print MAT TWO_DIM1$ !Normal (original) form
00360 !
00370 ! Convert to one dimension for sorting
00380 let DIM1 = UDIM(TWO_DIM1$,1) !:
let DIM2 = UDIM(TWO_DIM1$,2)
00390 mat TWO_DIM1$(DIM1 * DIM2) !Restructure to 1 dimension
00400 print MAT TWO_DIM1$ !same data restructured
00410 print
00420 print "Press Any Key..."
00430 let KSTAT$(1)
00440 !
00450 let KEY_COLUMN = 1
00460 mat WORK$(DIM1) !Space for row keys
00470 for X = 0 to DIM1-1
00480 let WORK$(X+1) = TWO_DIM1$(X*DIM2 +KEY_COLUMN) !Get keys
00490 next X
00500 mat INDEX(DIM1) = AIDX(WORK$) !Index rows
00510 mat TWO_DIM2$(DIM1 * DIM2) !Restructure target array
00520 !
00530 for X = 0 to DIM1 -1 !For each 'to' row base 0
00540 let Y = INDEX(X+1) -1 !Get 'from' row base 0
00550 mat TWO_DIM2$(X*DIM2 +1:X*DIM2 +DIM2) =
TWO_DIM1$(Y*DIM2 +1:Y*DIM2 +DIM2) !Copy sub array
00560 next X
00570 mat TWO_DIM1$(DIM1,DIM2) !Restore source array
00580 mat TWO_DIM2$(DIM1,DIM2) !Restructure target array
00590 print MAT TWO_DIM1$
00600 print
00610 print MAT TWO_DIM2$
MAT Grouping
MAT grouping is now allowed in all full screen-processing statements. This feature allows you to indicate that input or output should alternate between all MAT variables that are specified within parentheses in the I/O list.
In the following code fragment, the A$ variable identifies the positions on the screen from which input values should be drawn. As usual, Business Rules will assign the first input value to the first element of B$. However, because the B$ and C matrices are specified within parentheses, it will then assign the second input value to the first element of C. The third value will go to B$, the fourth to C, and so on until both matrices are fully assigned. The last input value will go to X$.
00020 INPUT FIELDS A$: (MAT B$,MAT C),X$
Without MAT grouping, the above line must be coded as follows in order to achieve the same results (this example assumes that B$ and C have each been dimensioned for five elements):
00020 INPUT FIELDS A$: B$(1),C(1),B$(2),C(2),B$(3),C(3),B$(4),C(4),B$(5),C(5),X$
MAT grouping is a lot easier to code, it executes faster, and most importantly it handles much larger arrays than are possible without using MAT grouping, as the resulting compiled line takes up less space in memory. The number of matrices that can be grouped together is 62, which in practical terms are no limit. All matrices in a group must have the same number of elements per matrix, or an error 0106 will result. Only MAT variables may be used in such groupings.
See error 0106 for additional information.